力扣-226.翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
1
2
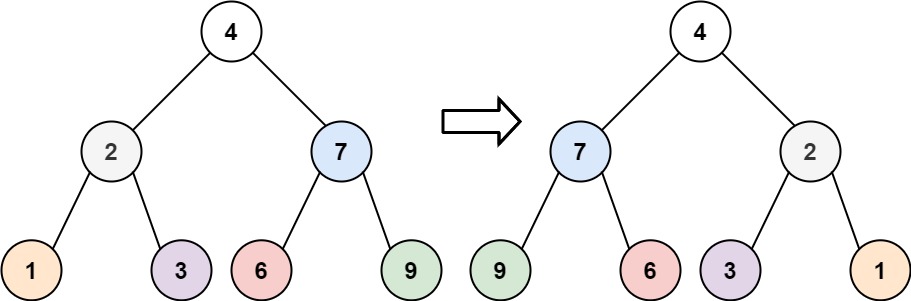
| 输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
|
示例 2:
1
2
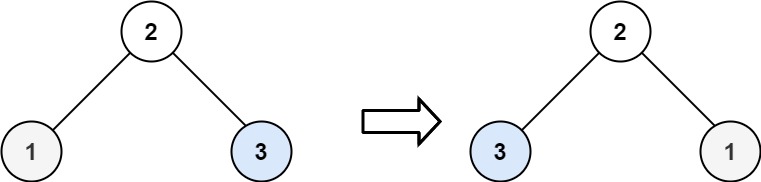
| 输入:root = [2,1,3]
输出:[2,3,1]
|
示例 3:
提示:
- 树中节点数目范围在
[0, 100] 内
-100 <= Node.val <= 100
解题思路
可以在遍历二叉树的过程中,对每个根节点,交换它的左右子树。但是需注意中序遍历无法实现,遍历过程中一直在处理左子树,右子树没有处理到。时间复杂度O(n),空间复杂度O(h)
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| // 1.递归法只能使用前序或后序,中序会导致一直处理左子树,右子树没处理到
var invertTree = function(root) {
if(root == null)
return null
// 保存右子树
const rightNode = root.right
// 将左子树移到右子树
root.right = invertTree(root.left)
// 将右子树移到左子树
root.left = invertTree(rightNode)
return root
};
// 2.迭代前序
var invertTree = function(root) {
const invertNode = function(root,left,right){
let tmp = left
left = right
right = tmp
root.left = left
root.right = right
}
// 前序遍历为根左右,则入栈顺序应为右左根,根节点会先出栈被处理
if(root == null)
return null
let stack = []
stack.push(root)
while(stack.length){
let node = stack.pop()
if(node !== null){
// 按右左根入栈
node.right && stack.push(node.right)
node.left && stack.push(node.left)
stack.push(node)
// 根节点入栈后push一个空节点做标记,出栈的时候空节点的下一节点即为根节点
stack.push(null)
}else{
// 处理根节点,交换根节点的左右子树
node = stack.pop()
invertNode(node,node.left,node.right)
}
}
return root
}
// 3.层序遍历
var invertTree = function(root) {
const invertNode = function(root,left,right){
let tmp = left
left = right
right = tmp
root.left = left
root.right = right
}
if(root == null)
return null
let queue = []
queue.push(root)
while(queue.length){
let levelLength = queue.length
while(levelLength--){
let node = queue.shift()
invertNode(node,node.left,node.right)
node.left && queue.push(node.left)
node.right && queue.push(node.right)
}
}
return root
}
|


